Describe the Continuity or Discontinuity of the Graphed Function

Infinity there is a vertical asymptote in the graph 4. We know that.

Lots Of Points Urgent Describe The Continuity Or Discontinuity Of The Graphed Function Brainly Com

Marusya05 52 10 months ago.

. In the given graphed function the graph is continous from x-6 to just left of x-2. The function has a vertical asymptote of x2 The function has a removable discontinuity of x-2 The function has a horizontal asymptote of y 0 No x intercept Y-intercept is 0-05 End Behavior fx -- 0 x. у 10 сл х 10 -10 -5 5 -5 -10 Use the graph to answer the question.

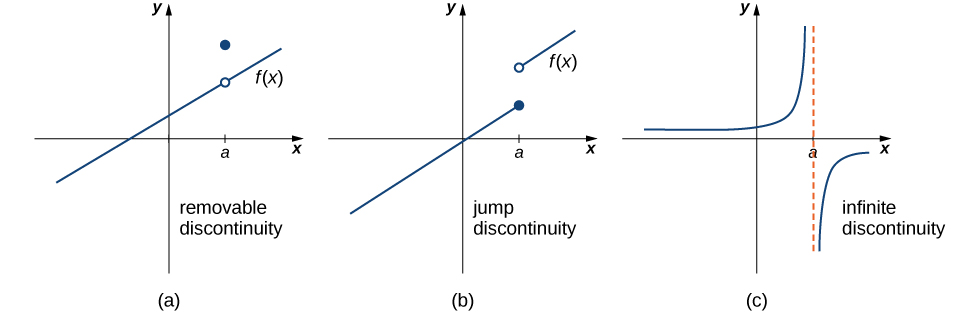
Describe the continuity of the graphed function. A function being continuous at a point means that the two-sided limit at that point exists and is equal to the functions value. Asymptoticinfinite discontinuity is when the two.

Jump discontinuity is when the two-sided limit doesnt exist because the one-sided limits arent equal. We can see that left limit is not equal to right. 1 point O The function has a removable discontinuity at x 3.

Use the graph to answer the question also the one I put in the attachment. We can see that this curve is smooth everywhere except at x3. If a function is not continuous at a point then we say it is discontinuous at that point.

Be sure to indicate the location of each discontinuity and identify the type. Precalculus questions and answers. If you remember the concept a function f x is continuous at x a if.

But at x-2 the continuity of graph is breaking because at x-2 the function has a value y1. The function has a removable discontinuity at x 0. The answer is A and C Step-by-step explanation.

Oscillating there is an infinite oscillation at a point in the graph Removable Discontinuity. The graph of the function is shown below for reference. A function has discontinuity where its continuity breaks.

I was looking for the whole function however it only asked for which interval is the function increasing on. In order to fix the discontinuity we need to know the y-value of the hole in the graph. The function is continuous.

You could tell by seeing the plot of a function that it has a discontinuity if you cant trace ir without lifting your pen from the sheet as you can see you have to lift your pen in x -1. Describe the continuity or discontinuity of the graphed function. Describe the continuity of the graphed function.

Quiz corrections Unit 3 lesson 6. The function below has a removable discontinuity at x 2. Find a possible formula for the function graphed below.

The function graphed below is NOT continuous everywhere it is discontinuous at x 2 and. For the example 2 given above we can draw the graph as given below. You can make it by math too.

Any function fx is continuous at xa only if. The function has a removable discontinuity at x 3. Fx fracx2-2xx2-4 Solution.

Continuity A function is a continuous at a point if its graph has no gaps holes breaks or jumps at that point. The function has a jump discontinuity at x 3. Assume the function has only one x-intercept at the origin and the point.

Any function fx is continuous at xa only if. Removable there is a hole in the graph 2. Then again its continuity is.

We can represent the continuous function using graphs. The correct answer is B because it is increasing at points -10 and 10 or 1infinity. The function has an infinite discontinuity at x 3.

Describe the continuity of the graphed function. Describe the discontinuity of the graphed function. Hence x 1 is the only point of discontinuity of f.

So we will check continuity at x3. Bezzdna 24 1 year ago. The function graphed below is continuous everywhere.

To determine this we find the value of limlimits_xto. Thus the function fx is not continuous at x 1. From just right of x-2 to just left of x-1 graph is continous.

Redefine the function so that it becomes continuous at x2. Common types of discontinuities 1. We can see that all three values are not equal.

We know that. Correct answer - Describe the discontinuity of the graphed function. Pointremovable discontinuity is when the two-sided limit exists but isnt equal to the functions value.

At x-5 we got a removable discontinuity because that point is removed there at x1 we got a jump or step discontinuity because the graph jumps there. The function has a nonremovable discontinuity at x 3. We can see that this curve is smooth everywhere except at x3.

Describe the continuity of the graphed function. So we will check continuity at x3. Dybincka 34 1 year ago.

In this graph we can clearly see that the function is not continuous at x 1. I put D -11U 1infinity. Jump there is a jump in the graph 3.

7 Continuous And Discontinuous Functions

Describe The Continuity Or Discontinuity Of The Graphed Function I Will Give More Points And Brainly Com

2 4 Continuity Calculus Volume 1